Binary GCD

In this section, we will derive a variant of gcd that is ~2x faster than the one in the C++ standard library.

#Euclid’s Algorithm

Euclid’s algorithm solves the problem of finding the greatest common divisor (GCD) of two integer numbers $a$ and $b$, which is defined as the largest such number $g$ that divides both $a$ and $b$:

This is true, because if $g = \gcd(a, b)$ divides both $a$ and $b$, it should also divide $(a \bmod b = a - k \cdot b)$, but any larger divisor $d$ of $b$ will not: $d > g$ implies that $d$ couldn’t divide $a$ and thus won’t divide $(a - k \cdot b)$.

The formula above is essentially the algorithm itself: you can simply apply it recursively, and since each time one of the arguments strictly decreases, it will eventually converge to the $b = 0$ case.

The textbook also probably mentioned that the worst possible input to Euclid’s algorithm — the one that maximizes the total number of steps — are consecutive Fibonacci numbers, and since they grow exponentially, the running time of the algorithm is logarithmic in the worst case. This is also true for its average running time if we define it as the expected number of steps for pairs of uniformly distributed integers. The Wikipedia article also has a cryptic derivation of a more precise $0.84 \cdot \ln n$ asymptotic estimate.

There are many ways you can implement Euclid’s algorithm. The simplest would be just to convert the definition into code:

int gcd(int a, int b) {
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}

You can rewrite it more compactly like this:

int gcd(int a, int b) {
    return (b ? gcd(b, a % b) : a);
}

You can rewrite it as a loop, which will be closer to how it is actually executed by the hardware. It won’t be faster though, because compilers can easily optimize tail recursion.

int gcd(int a, int b) {
    while (b > 0) {
        a %= b;
        std::swap(a, b);
    }
    return a;
}

You can even write the body of the loop as this confusing one-liner — and it will even compile without causing undefined behavior warnings since C++17:

int gcd(int a, int b) {
    while (b) b ^= a ^= b ^= a %= b;
    return a;
}

All of these, as well as std::gcd which was introduced in C++17, are almost equivalent and get compiled into functionally the following assembly loop:

; a = eax, b = edx
loop:
    ; modulo in assembly:
    mov  r8d, edx
    cdq
    idiv r8d
    mov  eax, r8d
    ; (a and b are already swapped now)
    ; continue until b is zero:
    test edx, edx
    jne  loop

If you run perf on it, you will see that it spends ~90% of the time on the idiv line. This isn’t surprising: general integer division works notoriously slow on all computers, including x86.

But there is one kind of division that works well in hardware: division by a power of 2.

#Binary GCD

The binary GCD algorithm was discovered around the same time as Euclid’s, but on the other end of the civilized world, in ancient China. In 1967, it was rediscovered by Josef Stein for use in computers that either don’t have division instruction or have a very slow one — it wasn’t uncommon for CPUs of that era to use hundreds or thousands of cycles for rare or complex operations.

Analogous to the Euclidean algorithm, it is based on a few similar observations:

1. $\gcd(0, b) = b$ and symmetrically $\gcd(a, 0) = a$;
2. $\gcd(2a, 2b) = 2 \cdot \gcd(a, b)$;
3. $\gcd(2a, b) = \gcd(a, b)$ if $b$ is odd and symmetrically $\gcd(a, b) = \gcd(a, 2b)$ if $a$ is odd;
4. $\gcd(a, b) = \gcd(|a − b|, \min(a, b))$, if $a$ and $b$ are both odd.

Likewise, the algorithm itself is just a repeated application of these identities.

Its running time is still logarithmic, which is even easier to show because in each of these identities one of the arguments is divided by 2 — except for the last case, in which the new first argument, the absolute difference of two odd numbers, is guaranteed to be even and thus will be divided by 2 on the next iteration.

What makes this algorithm especially interesting to us is that the only arithmetic operations it uses are binary shifts, comparisons, and subtractions, all of which typically take just one cycle.

#Implementation

The reason this algorithm is not in the textbooks is because it can’t be implemented as a simple one-liner anymore:

int gcd(int a, int b) {
    // base cases (1)
    if (a == 0) return b;
    if (b == 0) return a;
    if (a == b) return a;

    if (a % 2 == 0) {
        if (b % 2 == 0) // a is even, b is even (2)
            return 2 * gcd(a / 2, b / 2);
        else            // a is even, b is odd (3)
            return gcd(a / 2, b);
    } else {
        if (b % 2 == 0) // a is odd, b is even (3)
            return gcd(a, b / 2);
        else            // a is odd, b is odd (4)
            return gcd(std::abs(a - b), std::min(a, b));
    }
}

Let’s run it, and… it sucks. The difference in speed compared to std::gcd is indeed 2x, but on the other side of the equation. This is mainly because of all the branching needed to differentiate between the cases. Let’s start optimizing.

First, let’s replace all divisions by 2 with divisions by whichever highest power of 2 we can. We can do it efficiently with __builtin_ctz, the “count trailing zeros” instruction available on modern CPUs. Whenever we are supposed to divide by 2 in the original algorithm, we will call this function instead, which will give us the exact number of bits to right-shift the number by. Assuming that the we are dealing with large random numbers, this is expected to decrease the number of iterations by almost a factor 2, because $1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots \to 2$.

Second, we can notice that condition 2 can now only be true once — in the very beginning — because every other identity leaves at least one of the numbers odd. Therefore we can handle this case just once in the beginning and not consider it in the main loop.

Third, we can notice that after we’ve entered condition 4 and applied its identity, $a$ will always be even and $b$ will always be odd, so we already know that on the next iteration we are going to be in condition 3. This means that we can actually “de-evenize” $a$ right away, and if we do so we will again hit condition 4 on the next iteration. This means that we can only ever be either in condition 4 or terminating by condition 1, which removes the need to branch.

Combining these ideas, we get the following implementation:

int gcd(int a, int b) {
    if (a == 0) return b;
    if (b == 0) return a;

    int az = __builtin_ctz(a);
    int bz = __builtin_ctz(b);
    int shift = std::min(az, bz);
    a >>= az, b >>= bz;
    
    while (a != 0) {
        int diff = a - b;
        b = std::min(a, b);
        a = std::abs(diff);
        a >>= __builtin_ctz(a);
    }
    
    return b << shift;
}

It runs in 116ns, while std::gcd takes 198ns. Almost twice as fast — maybe we can even optimize it below 100ns?

For that we need to stare at its assembly again, in particular at this block:

; a = edx, b = eax
loop:
    mov   ecx, edx
    sub   ecx, eax       ; diff = a - b
    cmp   eax, edx
    cmovg eax, edx       ; b = min(a, b)
    mov   edx, ecx
    neg   edx
    cmovs edx, ecx       ; a = max(diff, -diff) = abs(diff)
    tzcnt ecx, edx       ; az = __builtin_ctz(a)
    sarx  edx, edx, ecx  ; a >>= az
    test  edx, edx       ; a != 0?
    jne   loop

Let’s draw the dependency graph of this loop:

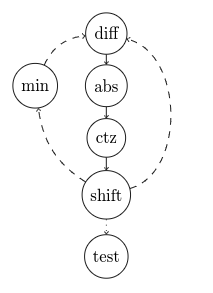
Modern processors can execute many instructions in parallel, essentially meaning that the true “cost” of this computation is roughly the sum of latencies on its critical path. In this case, it is the total latency of diff, abs, ctz, and shift.

We can decrease this latency using the fact that we can actually calculate ctz using just diff = a - b, because a negative number divisible by $2^k$ still has $k$ zeros at the end of its binary representation. This lets us not wait for max(diff, -diff) to be computed first, resulting in a shorter graph like this:

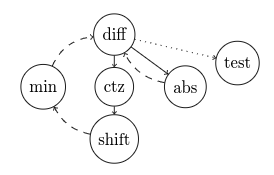
Hopefully you will be less confused when you think about how the final code will be executed:

int gcd(int a, int b) {
    if (a == 0) return b;
    if (b == 0) return a;

    int az = __builtin_ctz(a);
    int bz = __builtin_ctz(b);
    int shift = std::min(az, bz);
    b >>= bz;
    
    while (a != 0) {
        a >>= az;
        int diff = b - a;
        az = __builtin_ctz(diff);
        b = std::min(a, b);
        a = std::abs(diff);
    }
    
    return b << shift;
}

It runs in 91ns, which is good enough to leave it there.

If somebody wants to try to shave off a few more nanoseconds by rewriting the assembly by hand or trying a lookup table to save a few last iterations, please let me know.

#Acknowledgements

The main optimization ideas belong to Daniel Lemire and Ralph Corderoy, who had nothing better to do on the Christmas holidays of 2013.