How long does it take to add two numbers together? Being one of the most frequently used instructions, add by itself only takes one cycle to execute. So, if the data is already loaded into registers, it takes one just cycle.
But in the general case (*c = *a + *b), we need to fetch its operands from memory first:
mov eax, DWORD PTR [rsi]
add eax, DWORD PTR [rdi]
mov DWORD PTR [rdx], eax
When you fetch anything from memory, there is always some latency before the data arrives. Moreover, the request doesn’t go directly to its ultimate storage location, but it first goes through a complex system of address translation units and caching layers designed to both help in memory management and reduce latency.
Therefore, the only correct answer to this question is “it depends” — primarily on where the operands are stored:
- If the data is stored in the main memory (RAM), it will take around ~100ns, or about 200 cycles, to fetch it, and then another 200 cycles to write it back.
- If it was accessed recently, it is probably cached and will take less than that to fetch, depending on how long ago it was accessed — it could be ~50 cycles for the slowest layer of cache and around 4-5 cycles for the fastest.
- But it could also be stored on some type of external memory such as a hard drive, and in this case, it will take around 5ms, or roughly $10^7$ cycles (!) to access it.
Such a high variance of memory performance is caused by the fact that memory hardware doesn’t follow the same laws of silicon scaling as CPU chips do. Memory is still improving through other means, but if 50 years ago memory timings were roughly on the same scale with the instruction latencies, nowadays they lag far behind.
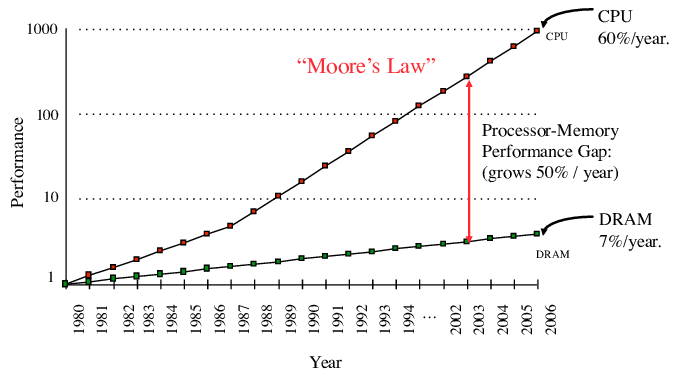
To be less of a limiting factor, modern memory systems are becoming increasingly hierarchical, where the higher layers trade off some of their capacity for reduced latency. As these characteristics may change in the orders of magnitude between the layers — especially in the case of external memory types — it became crucial for many memory-intensive algorithms to optimize their I/O operations before anything else.
This prompted the creation of a new cost model, called the external memory model, whose only primitive operations are block reads and writes, and everything else has zero cost as long as it only involves data stored in a limited-sized local memory. It spawned an exciting new field of external memory algorithms, which we will study in this chapter.