List Ranking

In this section, we will apply external sorting and joining to solve a problem that seems useless on the surface but is actually a key primitive used in a large number of external memory and parallel algorithms.

Problem. Given a singly-linked list, compute the rank of each element, equal to its distance from the last element.

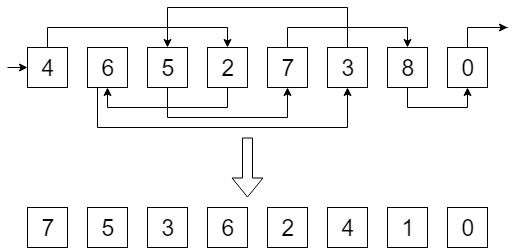
This problem can be trivially solved in the RAM model: you just traverse the entire list with a counter. But this pointer jumping wouldn’t work well in the external memory setting because the list nodes are stored arbitrarily, and in the worst case, reading each new node may require reading a new block.

#Algorithm

Consider a slightly more general version of the problem. Now, each element has a weight $w_i$, and for each element, we need to compute the sum of the weights of all its preceding elements instead of just its rank. To solve the initial problem, we can just set all weights equal to 1.

The main idea of the algorithm is to remove some fraction of elements, recursively solve the problem, and then use these weight-ranks to reconstruct the answer for the initial problem — which is the tricky part.

Consider some three consecutive elements $x$, $y$ and $z$. Assume that we deleted $y$ and solved the problem for the remaining list, which included $x$ and $z$, and now we need to restore the answer for the original triplet. The weight of $x$ would be correct as it is, but we need to calculate the answer for $y$ and adjust it for $z$, namely:

• $w_y’ = w_y + w_x$
• $w_z’ = w_z + w_y + w_x$

Now, we can just delete, say, the first element, solve the problem recursively, and recalculate weights for the original array. But, unfortunately, it would work in quadratic time, because to make the update, we would need to know where its neighbors are, and since we can’t hold the entire array in memory, we would need to scan it each time.

Therefore, on each step, we want to remove as many elements as possible. But we also have a constraint: we can’t remove two consecutive elements because then merging results wouldn’t be that simple.

Ideally, we want to split our list into even and odd elements, but doing this is not simpler than the initial problem. One workaround is to choose the elements at random: toss a coin for each element, and then remove all “heads” after which a “tail” follows. This way no two consecutive elements will ever be selected, and on average we get rid of ¼ of the current list. The arithmetic complexity of this solution would still be linear, because

The only tricky part here is how to implement the merge step in external memory. To do it efficiently, we need to maintain our list in the following form:

• List of tuples $(i, j)$ indicating that element $j$ follows after element $i$
• List of tuples $(i, w_i)$ indicating that element $i$ currently has weight $w_i$
• A list of deleted elements

Now, to restore the answer after randomly deleting some elements and recursively solving the smaller problem, we need to iterate over all lists using three pointers looking for deleted elements. and for each such element, we will write $(j, w_i)$ to a separate table, which would signify that before the recursive step we need to add $w_i$ to $j$. We can then join this new table with initial weights, add these additional weights to them.

After coming back from the recursion, we need to update weights for the deleted elements, which we can do with the same technique, iterating over reversed connections instead of direct ones.

I/O complexity of this algorithm with therefore be the same as joining, namely $SORT(N) = O\left(\frac{N}{B} \log_{\frac{M}{B}} \frac{N}{M} \right)$.

#Applications

List ranking is especially useful in graph algorithms.

For example, we can obtain the Euler tour of a tree in external memory by constructing a linked list from the tree that corresponds to its Euler tour and then applying the list ranking algorithm — the ranks of each node will be the same as its index $tin_v$ in the Euler tour. To construct this list, we need to:

• split each undirected edge into two directed ones;
• duplicate the parent node for each up-edge (because list nodes can only have one incoming edge, but we visit some vertices multiple times);
• route each such node either to the “next sibling,” if it has one, or otherwise to its own parent;
• and then finally break the resulting cycle at the root.

This general technique is called tree contraction, and it serves as the basis for a large number of tree algorithms.

The same approach can be applied to parallel algorithms, and we will cover that much more deeply in part II.