If you took some time to study the reference, you may have noticed that there are essentially two major groups of vector operations:
- Instructions that perform some elementwise operation (
+,*,<,acos, etc.). - Instructions that load, store, mask, shuffle, and generally move data around.
While using the elementwise instructions is easy, the largest challenge with SIMD is getting the data in vector registers in the first place, with low enough overhead so that the whole endeavor is worthwhile.
#Aligned Loads and Stores
Operations of reading and writing the contents of a SIMD register into memory have two versions each: load / loadu and store / storeu. The letter “u” here stands for “unaligned.” The difference is that the former ones only work correctly when the read / written block fits inside a single cache line (and crash otherwise), while the latter work either way, but with a slight performance penalty if the block crosses a cache line.
Sometimes, especially when the “inner” operation is very lightweight, the performance difference becomes significant (at least because you need to fetch two cache lines instead of one). As an extreme example, this way of adding two arrays together:
for (int i = 3; i + 7 < n; i += 8) {
__m256i x = _mm256_loadu_si256((__m256i*) &a[i]);
__m256i y = _mm256_loadu_si256((__m256i*) &b[i]);
__m256i z = _mm256_add_epi32(x, y);
_mm256_storeu_si256((__m256i*) &c[i], z);
}
…is ~30% slower than its aligned version:
for (int i = 0; i < n; i += 8) {
__m256i x = _mm256_load_si256((__m256i*) &a[i]);
__m256i y = _mm256_load_si256((__m256i*) &b[i]);
__m256i z = _mm256_add_epi32(x, y);
_mm256_store_si256((__m256i*) &c[i], z);
}
In the first version, assuming that arrays a, b and c are all 64-byte aligned (the addresses of their first elements are divisible by 64, and so they start at the beginning of a cache line), roughly half of reads and writes will be “bad” because they cross a cache line boundary.
Note that the performance difference is caused by the cache system and not by the instructions themselves. On most modern architectures, the loadu / storeu intrinsics should be equally as fast as load / store given that in both cases the blocks only span one cache line. The advantage of the latter is that they can act as free run time assertions that all reads and writes are aligned.
This makes it important to properly align arrays and other data on allocation, and it is also one of the reasons why compilers can’t always auto-vectorize efficiently. For most purposes, we only need to guarantee that any 32-byte SIMD block will not cross a cache line boundary, and we can specify this alignment with the alignas specifier:
alignas(32) float a[n];
for (int i = 0; i < n; i += 8) {
__m256 x = _mm256_load_ps(&a[i]);
// ...
}
The built-in vector types already have corresponding alignment requirements and assume aligned memory reads and writes — so you are always safe when allocating an array of v8si, but when converting it from int* you have to make sure it is aligned.
Similar to the scalar case, many arithmetic instructions take memory addresses as operands — vector addition is an example — although you can’t explicitly use it as an intrinsic and have to rely on the compiler. There are also a few other instructions for reading a SIMD block from memory, notably the non-temporal load and store operations that don’t lift accessed data in the cache hierarchy.
#Register Aliasing
The first SIMD extension, MMX, started quite small. It only used 64-bit vectors, which were conveniently aliased to the mantissa part of a 80-bit float so that there is no need to introduce a separate set of registers. As the vector size grew with later extensions, the same register aliasing mechanism used in general-purpose registers was adopted for the vector registers to maintain backward compatibility: xmm0 is the first half (128 bits) of ymm0, xmm1 is the first half of ymm1, and so on.
This feature, combined with the fact that the vector registers are located in the FPU, makes moving data between them and the general-purpose registers slightly complicated.
#Extract and Insert
To extract a specific value from a vector, you can use _mm256_extract_epi32 and similar intrinsics. It takes the index of the integer to be extracted as the second parameter and generates different instruction sequences depending on its value.
If you need to extract the first element, it generates the vmovd instruction (for xmm0, the first half of the vector):
vmovd eax, xmm0
For other elements of an SSE vector, it generates possibly slightly slower vpextrd:
vpextrd eax, xmm0, 1
To extract anything from the second half of an AVX vector, it first has to extract that second half, and then the scalar itself. For example, here is how it extracts the last (eighth) element,
vextracti128 xmm0, ymm0, 0x1
vpextrd eax, xmm0, 3
There is a similar _mm256_insert_epi32 intrinsic for overwriting specific elements:
mov eax, 42
; v = _mm256_insert_epi32(v, 42, 0);
vpinsrd xmm2, xmm0, eax, 0
vinserti128 ymm0, ymm0, xmm2, 0x0
; v = _mm256_insert_epi32(v, 42, 7);
vextracti128 xmm1, ymm0, 0x1
vpinsrd xmm2, xmm1, eax, 3
vinserti128 ymm0, ymm0, xmm2, 0x1
Takeaway: moving scalar data to and from vector registers is slow, especially when this isn’t the first element.
#Making Constants
If you need to populate not just one element but the entire vector, you can use the _mm256_setr_epi32 intrinsic:
__m256 iota = _mm256_setr_epi32(0, 1, 2, 3, 4, 5, 6, 7);
The “r” here stands for “reversed” — from the CPU point of view, not for humans. There is also the _mm256_set_epi32 (without “r”) that fills the values from the opposite direction. Both are mostly used to create compile-time constants that are then fetched into the register with a block load. If your use case is filling a vector with zeros, use the _mm256_setzero_si256 instead: it xor-s the register with itself.
In built-in vector types, you can just use normal braced initialization:
vec zero = {};
vec iota = {0, 1, 2, 3, 4, 5, 6, 7};
#Broadcast
Instead of modifying just one element, you can also broadcast a single value into all its positions:
; __m256i v = _mm256_set1_epi32(42);
mov eax, 42
vmovd xmm0, eax
vpbroadcastd ymm0, xmm0
This is a frequently used operation, so you can also use a memory location:
; __m256 v = _mm256_broadcast_ss(&a[i]);
vbroadcastss ymm0, DWORD PTR [rdi]
When using built-in vector types, you can create a zero vector and add a scalar to it:
vec v = 42 + vec{};
#Mapping to Arrays
If you want to avoid all this complexity, you can just dump the vector in memory and read its values back as scalars:
void print(__m256i v) {
auto t = (unsigned*) &v;
for (int i = 0; i < 8; i++)
std::cout << std::bitset<32>(t[i]) << " ";
std::cout << std::endl;
}
This may not be fast or technically legal (the C++ standard doesn’t specify what happens when you cast data like this), but it is simple, and I frequently use this code to print out the contents of a vector during debugging.
#Non-Contiguous Load
Later SIMD extensions added special “gather” and “scatter instructions that read/write data non-sequentially using arbitrary array indices. These don’t work 8 times faster though and are usually limited by the memory rather than the CPU, but they are still helpful for certain applications such as sparse linear algebra.
Gather is available since AVX2, and various scatter instructions are available since AVX512.
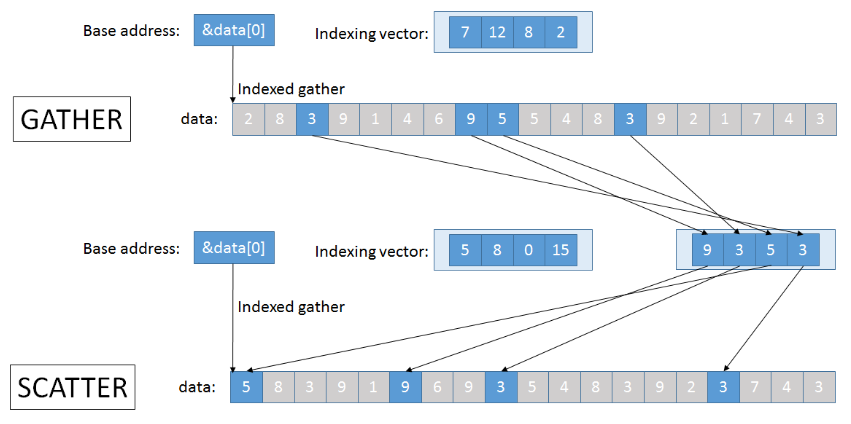
Let’s see if they work faster than scalar reads. First, we create an array of size $N$ and $Q$ random read queries:
int a[N], q[Q];
for (int i = 0; i < N; i++)
a[i] = rand();
for (int i = 0; i < Q; i++)
q[i] = rand() % N;
In the scalar code, we add the elements specified by the queries to a checksum one by one:
int s = 0;
for (int i = 0; i < Q; i++)
s += a[q[i]];
And in the SIMD code, we use the gather instruction to do that for 8 different indexes in parallel:
reg s = _mm256_setzero_si256();
for (int i = 0; i < Q; i += 8) {
reg idx = _mm256_load_si256( (reg*) &q[i] );
reg x = _mm256_i32gather_epi32(a, idx, 4);
s = _mm256_add_epi32(s, x);
}
They perform roughly the same, except when the array fits into the L1 cache:
The purpose of gather and scatter is not to perform memory operations faster, but to get the data into registers to perform heavy computations on them. For anything costlier than just one addition, they are hugely favorable.
The lack of (fast) gather and scatter instructions makes SIMD programming on CPUs very different from proper parallel computing environments that support independent memory access. You have to always engineer around it and employ various ways of organizing your data sequentially so that it be loaded into registers.
