Reductions

Reduction (also known as folding in functional programming) is the action of computing the value of some associative and commutative operation (i.e., $(a \circ b) \circ c = a \circ (b \circ c)$ and $a \circ b = b \circ a$) over a range of arbitrary elements.

The simplest example of reduction is calculating the sum an array:

int sum(int *a, int n) {
    int s = 0;
    for (int i = 0; i < n; i++)
        s += a[i];
    return s;
}

The naive approach is not so straightforward to vectorize, because the state of the loop (sum $s$ on the current prefix) depends on the previous iteration. The way to overcome this is to split a single scalar accumulator $s$ into 8 separate ones, so that $s_i$ would contain the sum of every 8th element of the original array, shifted by $i$:

If we store these 8 accumulators in a single 256-bit vector, we can update them all at once by adding consecutive 8-element segments of the array. With vector extensions, this is straightforward:

int sum_simd(v8si *a, int n) {
    //       ^ you can just cast a pointer normally, like with any other pointer type
    v8si s = {0};

    for (int i = 0; i < n / 8; i++)
        s += a[i];
    
    int res = 0;
    
    // sum 8 accumulators into one
    for (int i = 0; i < 8; i++)
        res += s[i];

    // add the remainder of a
    for (int i = n / 8 * 8; i < n; i++)
        res += a[i];
        
    return res;
}

You can use this approach for other reductions, such as for finding the minimum or the xor-sum of an array.

#Instruction-Level Parallelism

Our implementation matches what the compiler produces automatically, but it is actually suboptimal: when we use just one accumulator, we have to wait one cycle between the loop iterations for a vector addition to complete, while the throughput of corresponding instruction is 2 on this microarchitecture.

If we again divide the array in $B \geq 2$ parts and use a separate accumulator for each, we can saturate the throughput of vector addition and increase the performance twofold:

const int B = 2; // how many vector accumulators to use

int sum_simd(v8si *a, int n) {
    v8si b[B] = {0};

    for (int i = 0; i + (B - 1) < n / 8; i += B)
        for (int j = 0; j < B; j++)
            b[j] += a[i + j];

    // sum all vector accumulators into one
    for (int i = 1; i < B; i++)
        b[0] += b[i];
    
    int s = 0;

    // sum 8 scalar accumulators into one
    for (int i = 0; i < 8; i++)
        s += b[0][i];

     // add the remainder of a
    for (int i = n / (8 * B) * (8 * B); i < n; i++)
        s += a[i];

    return s;
}

If you have more than 2 relevant execution ports, you can increase the B constant accordingly, but the $n$-fold performance increase will only apply to arrays that fit into L1 cache — memory bandwidth will be the bottleneck for anything larger.

#Horizontal Summation

The part where we sum up the 8 accumulators stored in a vector register into a single scalar to get the total sum is called “horizontal summation.”

Although extracting and adding every scalar one by one only takes a constant number of cycles, it can be computed slightly faster using a special instruction that adds together pairs of adjacent elements in a register.

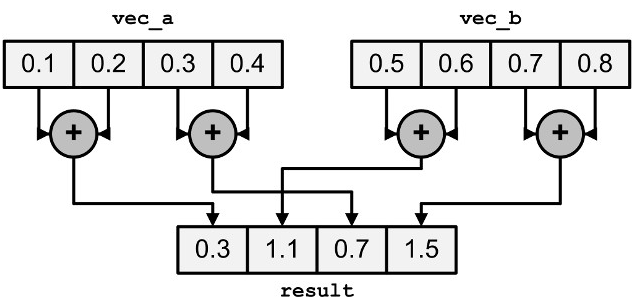
Since it is a very specific operation, it can only be done with SIMD intrinsics — although the compiler probably emits roughly the same procedure for the scalar code anyway:

int hsum(__m256i x) {
    __m128i l = _mm256_extracti128_si256(x, 0);
    __m128i h = _mm256_extracti128_si256(x, 1);
    l = _mm_add_epi32(l, h);
    l = _mm_hadd_epi32(l, l);
    return _mm_extract_epi32(l, 0) + _mm_extract_epi32(l, 1);
}

There are other similar instructions, e.g., for integer multiplication or calculating absolute differences between adjacent elements (used in image processing).

There is also one specific instruction, _mm_minpos_epu16, that calculates the horizontal minimum and its index among eight 16-bit integers. This is the only horizontal reduction that works in one go: all others are computed in multiple steps.