It is often beneficial to group together the data you need to fetch at the same time: preferably, on the same or, if that isn’t possible, neighboring cache lines. This improves the spatial locality of your memory accesses, positively impacting the performance of memory-bound algorithms.
To demonstrate the potential effect of doing this, we modify the pointer chasing benchmark so that the next pointer is computed using not one, but a variable number of fields ().
#Experiment
The first approach will locate these fields together as the rows of a two-dimensional array. We will refer to this variant as array of structures (AoS):
const int M = N / D; // # of memory accesses
int p[M], q[M][D];
iota(p, p + M, 0);
random_shuffle(p, p + M);
int k = p[M - 1];
for (int i = 0; i < M; i++)
q[k][0] = p[i];
for (int j = 1; j < D; j++)
q[i][0] ^= (q[j][i] = rand());
k = q[k][0];
}
for (int i = 0; i < M; i++) {
int x = 0;
for (int j = 0; j < D; j++)
x ^= q[k][j];
k = x;
}
And in the second approach, we will place them separately. The laziest way to do this is to transpose the two-dimensional array q and swap the indices in all its subsequent accesses:
int q[D][M];
// ^--^
By analogy, we call this variant structure of arrays (SoA). Obviously, for large ’s, it performs much worse:

The performance of both variants grows linearly with , but AoS needs to fetch up to 16 times fewer total cache lines as the data is stored sequentially. Even when , the additional time it takes to process the other 63 values is less than the latency of the first fetch.
You can also see the spikes at the powers of two. AoS performs slightly better because it can compute horizontal xor-sum faster with SIMD. In contrast, SoA performs much worse, but this isn’t about , but about , the size of the second dimension, being a large power of two: this causes a pretty complicated cache associativity effect.
#Temporary Storage Contention
At first, it seems like there shouldn’t be any cache issues as and the array is just too big to fit into the L3 cache in the first place. The nuance is that to process a number of elements from different memory locations in parallel, you still need some space to store them temporarily. You can’t simply use registers as there aren’t enough of them, so they need to be stored in the cache even though in just a microsecond you won’t be needing them.
Therefore, when N / D is a large power of two, and we are iterating over the array q[D][N / D] along the first index, some of the memory addresses we temporarily need will map to the same cache line — and as there isn’t enough space there, many of them will have to be re-fetched from the upper layers of the memory hierarchy.
Here is another head-scratcher: if we enable huge pages, it expectedly makes the total latency 10-15% lower for most values of , but for , it makes things ten times worse:

I doubt that even the engineers who design memory controllers can explain what’s happening right off the bat.
In short, the difference is because, unlike the L1/L2 caches that are private to each core, the L3 cache has to use physical memory addresses instead of virtual ones for synchronization between different cores sharing the cache.
When we are using 4K memory pages, the virtual addresses get somewhat arbitrarily dispersed over the physical memory, which makes the cache associativity problem less severe: the physical addresses will have the same remainder modulo 4K bytes, and not N / D as for the virtual addresses. When we specifically require huge pages, this maximum alignment limit increases to 2M, and the cache lines receive much more contention.
This is the only example I know when enabling huge pages makes performance worse, let alone by a factor of ten.
#Padded AoS
As long as we are fetching the same number of cache lines, it doesn’t matter where they are located, right? Let’s test it and switch to padded integers in the AoS code:
struct padded_int {
int val;
int padding[15];
};
const int M = N / D / 16;
padded_int q[M][D];
Other than that, we are still calculating the xor-sum of padded integers. We fetch exactly cache lines, but this time sequentially. The running time shouldn’t be different from SoA, but this isn’t what happens:

The running time is about ⅓ lower for , but this only applies to arrays that exceed the L3 cache. If we fix and change , you can see that the padded version performs slightly worse on smaller arrays because there are less opportunities for random cache sharing:

As the performance on smaller arrays sizes is not affected, this clearly has something to do with how RAM works.
#RAM-Specific Timings
From the performance analysis point of view, all data in RAM is physically stored in a two-dimensional array of tiny capacitor cells, which is split into rows and columns. To read or write any cell, you need to perform one, two, or three actions:
- Read the contents of a row in a row buffer, which temporarily discharges the capacitors.
- Read or write a specific cell in this buffer.
- Write the contents of a row buffer back into the capacitors so that the data is preserved and the row buffer can be used for other memory accesses.
Here is the punchline: you don’t have to perform steps 1 and 3 between two memory accesses that correspond to the same row — you can just use the row buffer as a temporary cache. These three actions take roughly the same time, so this optimization makes long sequences of row-local accesses run thrice as fast compared to dispersed access patterns.
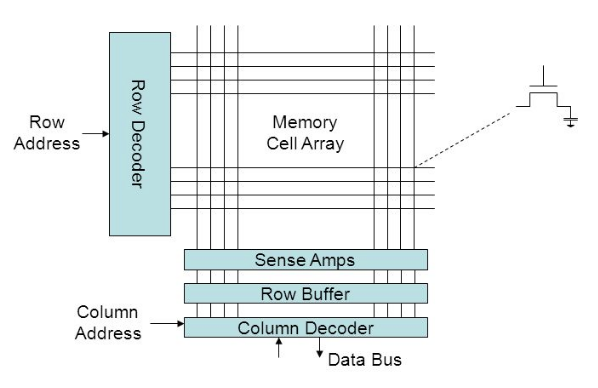
The size of the row differs depending on the hardware, but it is usually somewhere between 1024 and 8192 bytes. So even though the padded AoS benchmark places each element in a separate cache line, they are still very likely to be on the same RAM row, and the whole read sequence runs in roughly ⅓ of the time plus the latency of the first memory access.